+1(209) 348-9544
order@myessayservices.com
+1(209) 348-9544
order@myessayservices.com
Are you in High School, College, Masters, Bachelors or Ph.D and need someone to help in your homework? All you need is to ask for research paper help written by a specialist in your academic field. When you buy an essay online from My Essay Services, we offer you an original, nil plagiarized and unique paper written by a dedicated writer who is PhD or Masters qualified. MyEssayServices.com is an experienced service with over 9 years experience having delivered over 83,000 essays over the years.
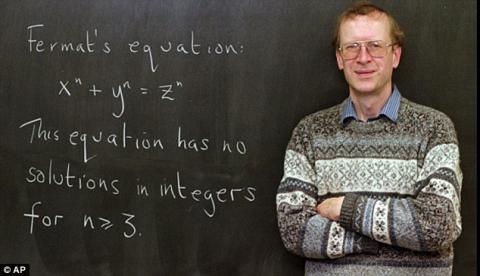Andrew Wiles were born in a family of academicians in 1953. His father was a professor of divinity working in Oxford University. The background of the mathematician led to the development of more interest in the studies. He was an excellent student in all the subjects. However, he developed more interests in mathematics from a tender age (Aczel, 1-52). To Andrew Wiles, mathematics was more than a subject or a requirement for the success in the classwork. To him, mathematics was more of a hobby (Apostol, 36). He loved the challenges that came with the subject.
He could complete all his homework to formulate new mathematical problems that he later solved. Being able to work on the mathematical issues was a source of satisfaction for the young mathematician. Being able to work on the problems also developed the research interest in him whereby it later formed the foundation of the research work and interests. He started his research on the mathematic problems by renting out books in the neighboring library. He used the books to find new problems. Most often, he used to look for the problems that were above his grade level. His preparedness in the mathematics field led to constantly excelling. The continued success of the young student cemented the interest and love of the student in the subject.
Early education
Wiles rented out books on Fermat theorem from the library more often than other books. The dedication to the understanding of the theorem led to the understanding of the concepts that formed the foundation of the assertion. The Fermat theorem was representative of a mathematic problem that had never been solved for over 300 years (Apostol, 36). The young student focused on how to improve on the theorem. He was only ten years when he started evaluating the issue. However, he was confident enough to provide his insights on the solution to the problem. He owned up the problem and sought out ways of solving it in the most optimal manner. He focused on the creation of the solution to the problem regardless of the tender age and the limited level of mathematical knowledge that he had acquired in the short time he had been in the school. He supposed that the solution to the problem would be arrived at in an easy way.
However, the research and all the efforts that he had invested in the solution of the problem were indicative that the opposite was true regarding the issue. He acknowledged that the problem needed more learning and understanding. Therefore, he understood that he needed to find new sources of knowledge that would enable him find the optimal solution to the problem actual solution to the problem need more understanding of other mathematic concepts that he did not have at the age (Apostol, 36).
His pursuit of the solution and the commitment to come up with the right solution to the issue later led to the acknowledgement of the need for other concepts of mathematics it also led to the understanding that the mathematics concepts were interconnected. Therefore, mathematical thinking had to assume a holistic approach (Aczel, 24-45). More importantly, it sowed the initial seeds of desire to pursue mathematics in the high levels of learning. The idea led to the creation of a lifetime commitment to the understanding of mathematics in order to provide solutions to similar issues.
In the formal education system, he was a constant performer in the common subjects required at his level of learning. He performed at an above average level in the rest of the subjects. In mathematics, he performed at consistently excellent level (Aczel, 142). His commitment to the discipline and the ability to challenge himself to do better in something that had defeated many mathematicians is indicative of the level of self-efficacy that young Wiles displayed. His dedication to excellence in mathematics was the main reason for his continued success in the class work relating to the same subject (Kleiner, 19-37).
Being able to live on the university campus also contributed to his budding of interest in the subject since he could meet with bright people who were willing to help him in his quest for better understanding of the theorem ('Invitation To The Mathematics Of Fermat-Wiles', 1). The staff at the local library also helped in the expansion of more understanding on the same issue. Their accommodating approach to the young researcher and willingness to assist him in finding what he needed to read in order to excel in mathematics and other disciplines helped in the growth of a more adept understanding of the subject matter. Their assistance in the initial research stages helped in the location and understanding of literature on the subject matter. They also helped in the development of the researching techniques (Apostol, 36).
Therefore, the environment in which he spent his formative years contributed to the budding of interest in mathematics and research. Support from his family was also a vital contributor to the mathematical interest. His father, who was a humanity professor, did not fault the decision of his son to pursue mathematics (Singh, 56). He did not attempt to push him towards his discipline. On the contrary, he tried to understand the interest of his son even when it was difficult to decipher what he was talking about. His moral support and encouragement contributed to the outcome of the young mathematician (Apostol, 36).
Later education
Andrew Wiles attended King's College School in Cambridge during his childhood. He proceeded to Merton College for his Bachelor’s Degree majoring in his favorite subject of mathematics. He received his Ph.D. in the same area of study in 1980. He conducted his postgraduate research at Clare College.
Career
Andre received an offer from Princeton University for an associate professorship. He took the position from 1981 to 1985 when Guggenheim appointed hams as a fellow. He worked in Paris for Guggenheim. He proceeded to Oxford in 1988 to work as a research professor in 1988 to 1990. He went back to Princeton as a tutor until 2011 after which he returned to Oxford.
Fermat last theorem
Andrew focused on his studies in line with his commitment to finding new knowledge that would help him solve the problem. At the age of 33, he felt that he had attained the needed knowledge to start working on the theorem once again ('Invitation To The Mathematics Of Fermat-Wiles', 1). He embarked on the research once again from 1986 to 1993. He found a solution to the problem and presented the proof to the public in the same year he had completed working on the theorem.
However, his first proof had an issue that made it inadmissible to the public. Working on the theorem had proved to be a journey marked with setbacks. He worked hard on the theorem to find the source of the problem. He reworked on the theory in the months after the issue in the proof was identified. He worked on the creation of a more in-depth understanding of the issue at hand. He later arrived at the solution to the error in his initial proof in 1994. His commitment to the proof rectification and the solution to the theorem led to the final success. Various inquests into the theorem indicated that the most famous mathematicians were not capable of finding any fault in the proof of the theorem.
Finally, his commitment to the theorem paid off since after publication of the proof; he was now famous. He had completed an inquest that he set out to do in his formative years, and the inquest had finally paid off. His contributions had led to the discovery of the solution to a problem that defeated even the brightest mathematicians in the history for three hundred years. His contributions to the finding of the proof of the theorem are important in the Mathematical discipline. He increased the value of the study of the annals of mathematics by finding the proof of the Fermat theorem.
Awards and distinctions
There are numerous inquests in the process that he used in coming up with the proof of the theorem. Most of the interviewers ask him about his motivations and challenges in finding the proof. They also ask about the source of the error in the initial proof. He has a permanent membership in the prestigious United States National Academy of Sciences. He also has numerous recognition and awards such as the Schlock Award of 1995, King Faisal Award of 1998, Pythagoras Award of 2004 and Shaw Award of 2005.
Work cited
Aczel, Amir D. Fermat's Last Theorem. New York: Four Walls Eight Windows, 1996. Print.
Apostol, Tom M. 'Ode To Andrew Wiles, Kbe'. The Mathematical Intelligencer 22.4 (2000): 36-36. Web.
'Invitation To The Mathematics Of Fermat-Wiles'. Choice Reviews Online 39.11 (2002): 39-6474-39-6474. Web.
Kleiner, Israel. 'From Fermat To Wiles: Fermat's Last Theorem Becomes A Theorem'. Elem. Math. 55.1 (2000): 19-37. Web.
Singh, Simon. Fermat's Enigma. New York: Walker, 1997. Print.
Table of Contents and outline
George Boole’s early years
Career development
Boole’s contribution and achievements
Boole’s marriage and personal life
George Boole’s influencers
Death
Boole’s Legacy
References
George Boole’s early years
George Boole, born on November 2, 1815, played a crucial role in facilitating the advanced computer and digital systems architecture. He was an English mathematician. He attended a National Society primary school where he later joined a school for commercial subjects. Apparently, the school of commercial subject marked the end of his formal education. However, similar to the father, he had a great skill of self-study. It was during that period, precisely at the age of 16 years, when he became an assistant teacher of an elementary school at Lincoln. After working in the school, he gained enough experienced that pushed him to opening up his own school four years later where he taught mathematics (Lambert 25).
Despite the father’s great study-skills, while he was working as a cobbler, he had strong passion and dedication to learning science and technology. He loved participating in Lincoln Mechanics’ Institution that promoted discussion and lectures related to science and technology (Gowers 44). Apparently, the role played by George’s father in the library as the curator supported Boole’s access to books. It was through the supportive family that Boole got the opportunity of advancing his knowledge of mathematics. Due to his growing interest in Mathematics, he had a discontentment with textbooks and forcibly began reading Laplace for mathematic ideas. His first work written from ideas collected was on variation calculus (Stanoyevitch 47).
Career development
After handing on his first work to Cambridge Mathematical Journal, the publisher (Duncan Gregory) got a positive impression of the ideas where he published them on the journal. Boole later following the impressive research work one by George, the publisher recommended him at Cambridge University. However, he declined the offer as he used teaching at his school as the sole source of financial support for his family (Khatri 35).
Boole’s consideration of the recommendation request at Cambridge University contributed to his decision of joining the university and immediately began studying algebra. In 1849, he became a mathematics professor at Queens College. Later, due to his impressive work, he became the dean of Science in the college (Lambert 64).
Boole’s contribution and achievements
By 1839, George produced his own mathematical work. His work inspired other scientists such as Albert Einstein. His major achievement was on 1841 when he developed the invariant theory. The invariant theory contributed to the study of intrinsic properties of polynomials in mathematics. In his theory, he postulate study mechanism of factors such as factorability, multiplicities of roots and as well geometrical congruentation of roots (Gowers 28).
Attributed to his great interests in mathematical operations, in 1844, he developed a pioneering paper on “Calculus of Operators.” The paper established his reputation among mathematicians. It was one of the major mathematic works during that period as it won the Royal Society’s gold medal (Lambert 22).
Additionally, as one of the most significant achievement in the computer science field, in 1847, he developed an interrelationship between logical problems and algebra. He applied algebra while solving logical problems (Khatri 66). It was in his work of “The Mathematical Analysis of Logic (Stanoyevitch 58). In his argument, he expanded knowledge by Leibniz’ the correlation between logic and math. Boole highlighted that logic is a mathematical discipline. It is in contrast with an earlier postulation that placed it under philosophy. Logic and algebra relationships contributed to Boolean algebra, which is the founding block for digital system design and computer architecture. The algebra is essential in modern systems as it calculates real values from a series of logically connected statements. Boolean algebra uses governing laws called Boolean laws. Boole developed the idea of true and false logical statements based on circuit functions (Gowers 36).
Boole’s marriage and personal life
He married Mary Everest in 1855 who was the daughter to George Everest. His study-skill motivation prevailed in their family where he encouraged his wife to continue studying at a local university. They successfully had five daughters together. They included; Mary Boole, Margaret Boole, Alice Boole, Lucy Boole and Ethel Boole s (Stanković 40).
George Boole’s influencers
His success in science and technology innovations had a basis on works from other scientist and family members. The major role player was his father who facilitated his access to library materials. More so, his great interests studying attributes to the exposure developed by the father. Another important individual was Leibniz’ who had a belief on existence of a relationship between logic and mathematics. He influenced Boole’s work on “Mathematical Analysis of Logic.” The idea of Boolean algebra was an expansion of Leibniz’s idea. Lagrange, on the other hand, through his great work of analytical mechanics versified Boole’s knowledge on mechanics (Stanoyevitch 22). Concepts learnt from Lagrange’s work were some of the building basics of George great works. Related to Lagrange was Laplace and his celestial mechanics works. His analysis utilized calculus while explaining star motions. Boole saw the knowledge vital in his understanding of calculus and sure, it was as it won him a gold award. Lastly, Gregory played vital roles in publishing his works in the Cambridge journal.
Death
Boole succumbed to pneumonia contracted after wearing wet clothes during a lecture. His death was on December 8, 1864 Ireland (Khatri 90). His funeral, held in the Church of Ireland, attracted many people from the community as they commemorated the great work by the scientist. In memory of Boole, Great Hall of University College made memorial window arts. These arts majorly commemorates the logical mathematics.
Boole’s Legacy
Boole’s work is a major building and contributor towards the modern technology advancements. Modern electronics continue utilizing his symbolic mathematical logics. Electrical circuits used utilize his Boolean algebra concept. The first application of the Boolean algebra was on 1930’s when Shannon developed switching circuits (Stanković 33). Nowadays, computers have their operations based on the Boolean algebra. His achievement is as well a major trigger towards the development of internet. Often internet searches such as Google use Boolean operators while differentiating search terms. Similarly, continued digitalization of systems uses his concepts of logical mathematics. An example is its application in the design of electromagnetic relay systems used in the telephony industry.
Reference
Stanković, Radomir S, and Jaakko Astola. From Boolean Logic to Switching Circuits and Automata: Towards Modern Information Technology. Berlin: Springer, 2011. Internet resource.
Khatri, Sunil P, and Kanupriya Gulati. Advanced Techniques in Logic Synthesis, Optimizations and Applications. New York: Springer, 2011. Internet resource.
Stanoyevitch, Alexander. Discrete Structures with Contemporary Applications. Boca Raton, FL: CRC Press, 2011. Print.
Lambert, Kevin. "Victorian Stained Glass As Memorial: An Image of George Boole." Visions of the Industrial Age, 1830 - 1914 / Ed. by Minsoo Kang and Amy Woodson-Boulton. (2008): 205-226. Print.
Gowers, Timothy, June Barrow-Green, and Imre Leader. The Princeton Companion to Mathematics. Princeton: Princeton University Press, 2008. Internet resource.
